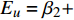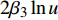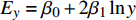Greenhouse Effect of Urbanization in China
-
摘要: 使用2003—2016年的省级面板数据,基于门限回归模型分析了我国城市化进程与温室气体排放的关系。根据门限变量人均实际GDP将30个省份内生分为4组。研究表明,4组的城市化与碳排放的关系都符合库兹涅茨曲线的倒U型形状。其中,低收入与中低收入两组的拐点对应的城市化水平分别是35.55%和44.64%。高收入组经济增长与碳排放之间呈现的是库兹涅茨曲线形状,而且处于倒U型曲线的下降阶段。此外,工业化进程与节能减排投资仍表现为对碳排放的扩张效应。因此,现阶段中国节能减排战略应遵循一定的经济和社会发展规律,考虑到不同省份的经济发展水平、发展速度以及城市化程度对碳排放的不同影响,兼顾经济发展与环境规制的双重目标。Abstract: Based on provincial panel data from 2003 to 2016, the relationship between urbanization and carbon emission in China was studied by constructing a threshold regression model. According to the threshold of real GDP per capita, 30 provinces are divided into four groups of lowest-income, lower-income, higher-income and highest-income. The results show that the relationship between urbanization and carbon emissions of four groups is in line with the Kuznets curve of inverted U shape. Among them, the inflection point corresponds to an urbanization level of 35.55% for the lowest-income group and to 44.64% for the lower-income group. For the highest-income group (more than RMB 29 040 yuan), the relationship between economic growth and carbon emission conforms to the Kuznets curve, and it is in the downward phase of an inverted U curve. In addition, the process of industrialization and investment of energy-saving and emission reduction are still promoting carbon emissions. Therefore, China’s energy conservation and emission reduction strategy should follow the law of economic and social development, considering the varying effects of the economic development level, development speed, and degree of urbanization of different provinces on carbon emissions, taking into account the dual goals of economic development and environmental regulation.
-
1978年以来,中国处于城市化与工业化的快速进程之中。中国人口城市化率以每年约1%的速度增加[1]。截至2018年,我国城镇人口占总人口的比例达到了59.58%。人口城市化会带来产业活动的规模集中,消耗大量的能源资源,产生CO2排放。2007年中国的CO2排放总量高达67.2亿t,超过美国成为全球CO2排放最多的国家。2013年中国的碳排放量更是达到了100亿t,超过了欧盟和美国的总和[2]。研究中国城市化的温室效应,具有非常重要的现实意义。
一. 文献综述
国外有关城市化与碳排放关系的研究成果丰富,研究范围较广,涉及城市形态、城市生活方式和人口城市化等方面[3-4]。大多数研究认为,人口不断向城市集聚带来的城市人口比重增加,会引起产业结构、就业结构和生活方式的巨大改变,从而引起碳排放的变化[5-6]。另外,部分研究也认为城市化与碳排放的关系依赖于经济发展水平和人均收入高低,收入有差异、发展程度有区别,二者的关系就会不同[7-9]。新常态下,中国城市化进程在促进经济增长的同时,也会使整体能源消费水平提高,从而导致碳排放总量的增长[10]。
国内研究主要着眼于城市化变量及其他控制变量对碳排放的影响机理,使用的研究方法是Kaya等式、IPAT模型或者它的随机形式STIRPAT模型。涉及到的控制变量包括人均财富水平或经济发展程度、产业结构或工业化水平、能源技术水平等。人均财富或经济发展水平一般以人均GDP作为代理变量,从而验证环境库兹涅茨曲线的形状及拐点[11];产业结构或工业化一般以工业增加值或者第二、三产业比值作为代理变量[12]。能源技术水平一般以能源强度,即能源使用量与GDP的比值作为代理变量[13]。
城市化对碳排放的影响随着收入水平或者发展阶段等控制变量的不同而变化,在使用截面数据或面板数据研究时就会面临样本数据的异质性问题。部分研究会从不同的出发点将数据样本拆分成几部分,如按照年平均碳排放水平将中国30个省区分成5组[14];Wang等[15]依据人均国民收入将全国省区分成3部分;更为常见的是按照省市的地理位置划分为东部、中部和西部3类[16]。上述对样本的处理最大的局限在于分组变量的选择过于主观,且变量阈值不是客观选择的。这就很大程度上隐藏了样本信息所反映的研究对象本身具有的异质性,并且存在两个弊端:①利用重新分组后的子样本进行回归,样本数量的减少降低了估计结果的准确性;②分组后的样本省份不能随着分组变量值的变动而改变所属的子样本组,这就忽视了样本省份的动态变化。针对于此,少数文献考虑到了异质性问题,如Ehrhardt-Martinez K[17]采用半参数混合潜类模型(latent class models)将所研究的国家分为3组。
与现有文献相比,本文的贡献有两点:①利用面板门限回归模型对省际样本做了内生分组,其优势在于允许省份在样本期内根据门限变量值的变化而归属于不同的分组,从而对不同省份城市化的温室效应进行了更加科学而准确的分析;②区别于已有文献,使用第二产业与第一产业的比值作为工业化的代理变量,使用国有能源工业固定资产投资作为节能减排投资的代理变量,来分析不同控制变量约束下城市化建设对碳排放水平的影响。
二. 理论模型和数据样本
一 计量模型
1 基础模型
本文的实证分析模型为:
$$\begin{aligned} \ln {C_{it}} = & {\delta _i} + {\beta _0}\ln {y_{it}} + {\beta _1}\ln y_{it}^2 + {\beta _2}\ln {u_{it}} + {\beta _3}\ln u_{it}^2 + \\ & {\beta _4}\ln {e_{it}} + {\beta _5}\ln s_{21it} + {\phi _t} + {\varepsilon _{it}} \\ \end{aligned} $$ (1) 式中,因变量为各省份CO2的排放量C,主要是由于该指标具备能够反映各省份从碳排放角度考察的温室效应总水平的总体代表性和不随人口数量改变而改变的时间可比性[18]。
核心解释变量为城市化变量u。考虑到数据的可获取性及权威性,本文采用众多文献中的做法,利用城市人口占总人口的比例作为城市化的衡量指标。也有文献使用非农业人口占总人口的比例来衡量城市化水平[1],但这样处理,可能会降低城市化对城市建设用地扩张的影响。控制变量之一是人均实际GDP(y),作为人均财富或经济发展水平的代理变量。控制变量之二是产业结构变量或工业化变量s21。选用第二产业与第一产业产值的比值作为代理变量,这与绝大多数研究中使用第二产业占GDP的比值作为工业化的代理变量不同。这克服了后者仅仅表征一个地区内部工业再生的能力以及工业的专业化水平,用来描述整体工业化程度并不贴切。Chenery等[19]的实证研究表明,用第二产业与第一产业的比值来表征国家的工业化水平会更加准确。控制变量之三是节能减排投资技术变量e,本文使用国有能源工业固定资产投资作为代理变量。长期以来,中国的能源工业主要是国有控股的企业,节能减排投资主要是这些国有能源企业的固定资产投资。因此,为了克服节能减排投资数据的不可获得性,本文使用国有能源工业固定资产投资作为节能减排投资的代理变量,来考察我国省份之间节能减排投资效果的差异。
根据Richard等[20]和Ehrhardt-Martinez K[17]的现代化理论,本文在模型中引入人均实际GDP和城市化水平的平方项,来观察经济发展与城市化对碳排放的非线性影响,从而验证中国省份经济发展和城市化的环境库兹涅茨曲线(Environmental Kuznets Curve,简称EKC)[21-22]的存在。
式(1)中,
${\delta _i}$ 代表因环境规制程度、能源资源禀赋等引致的省份区域差异;${\phi _t}$ 代表外部环境中的世界能源价格和节能技术变革给全国所有省市带来的外生时间效应;$i$ 和t依次表征省份和时间。2 门限回归模型
本文使用了门限回归模型[23],其优势在于根据特定门限变量对样本进行分组回归,并允许截面在样本期内根据门限变量值在分组间转移变化,是比EKC曲线更灵活的非线性形式。
门限回归模型的基础特征为:假设只存在一个门限变量
$t$ ,而且这个变量只存在2个阈值${\gamma _1},{\gamma _2}$ ,则模型为:$$ \begin{aligned} \ln {C_{it}} = & {\delta _i} + {{{\beta}} '_1}{{{x}}_{it}}d({t_{it}} \leqslant {\gamma _1}) + {{{\beta}} '_2}{{{x}}_{it}}d({\gamma _1} < {t_{it}} \leqslant {\gamma _2}) + \\ & {{{\beta}} '_3}{{{x}}_{it}}d({t_{it}} \geqslant {\gamma _2}) + {\varepsilon _{it}} \end{aligned} $$ (2) 式中,系数向量
${{{\beta}} '_i} = [{\beta _{0i}},{\beta _{1i}},{\beta _{2i}},{\beta _{3i}},{\beta _{4i}},{\beta _{5i}}]$ ,${\beta _{ki}}$ 为解释变量在第i个分组的系数;解释变量向量${{{x}}_{it}} = [\ln {y_{it}},$ $\ln y_{it}^2,\ln {u_{it}},\ln u_{it}^2,\ln {e_{it}},\ln s_{21it}]'$ ,$d({t_{it}} \leqslant {\gamma _1})$ ,$d({\gamma _1} < {t_{it}} \leqslant {\gamma _2})$ ,$d({t_{it}} \geqslant {\gamma _2})$ 是阈值产生的3个哑变量,如果门限变量$t$ 的值使之后的不等式成立就取值为1,否则取值为0。二 数据样本
本文CO2排放量的计算公式为:
$$C = \sum\limits_k {{\rm{GH}}{{\rm{G}}_k} \times {\rm{GW}}{{\rm{P}}_k}} $$ (3) $${\rm{GH}}{{\rm{G}}_k} = \sum\limits_{j = 1}^8 {{\rm{F}}{{\rm{E}}_j}} \times {\rm{NC}}{{\rm{V}}_j} \times {\rm{E}}{{\rm{F}}_{jk}}$$ (4) 这里,
${{\rm{GH}}{{\rm{G}}_k}}$ (k=1,2,3)是3种温室气体(CO2、NH4和N2O)所产生的碳排放量,${{\rm{GW}}{{\rm{P}}_k}}$ 为各温室气体对应的全球变暖潜能值,${{\rm{F}}{{\rm{E}}_j}}$ 是第j种化石能源的终端消费总量,${\rm{NC}}{{\rm{V}}_j}$ 是第j种传统能源的平均低位发热值,${\rm{E}}{{\rm{F}}_{jk}}$ 是第j种传统能源产生第k种温室气体的缺省排放因子。C计算单位为百万t。考虑到能源统计中没有涵盖西藏自治区和港澳台,因此数据处理时只采用了我国其余30个省(市、自治区)2003—2016年的数据进行分析。人均实际GDP是以2003年为不变价格进行计算,单位为元。文中人均实际GDP计算过程中使用的名义GDP以及指数数据、人口数据来自《中国统计年鉴》。国有能源工业固定资产投资数据来自《中国能源统计年鉴》,单位为万元。而人口城市化、第二产业、第一产业的数据主要来自《中国统计年鉴》;因统计口径不一致,2003、2004年的数据是笔者根据2004、2005年《中国统计年鉴》和《新中国60年统计资料》整理而来。实证研究的计算软件是Stata 14。三. 实证分析和结果讨论
一 平稳性检验
本研究的实证数据是来自30个省(市、自治区)14年的面板数据,为避免伪回归结果,首先做相关的平稳性检验。表1分别做了同单位根的LLC检验(Levin-Lin-Chu unit-root test)和异单位根的IPS检验(Im-Pesaran-Shin unit-root test)。
表 1 面板单位根检验变量 LLC同单位根检验 IPS异单位根检验 水平序列 一阶差分序列 水平序列 一阶差分序列 lnC −7.838
(0.010)−16.537
(0.000)−1.397
(0.718)−2.733
(0.000)lnu −6.167
(0.000)−17.225
(0.000)−1.597
(0.305)−2.702
(0.000)lnu2 −6.551
(0.000)−16.675
(0.000)−1.543
(0.415)−2.630
(0.000)lny −4.005
(0.594)−14.297
(0.002)−1.025
(0.995)−2.410
(0.000)lny2 −5.297
(0.045)−18.029
(0.000)−1.120
(0.981)−3.102
(0.000)lne −9.332
(0.000)−17.998
(0.000)−1.656
(0.203)−2.940
(0.000)lns21 −7.279
(0.002)−12.758
(0.000)−1.499
(0.509)−2.284
(0.000)注:表中的数值为Z统计量值,括号内为相应的P值。 LLC检验和IPS检验的原假设都是单位根存在。表1结果显示,除了人均实际GDP(y)的对数外,其他变量水平序列上的LLC检验都在一定程度上拒绝了原假设;而一阶差分序列上,两种检验方法都表明所有变量是平稳的,也即存在一阶单整。
二 相关估计方法的回归结果
为了便于比较以及保证回归结果的稳健性,笔者对全部样本依次采用了混合普通最小二乘估计(Pooled-OLS,简称POLS)、随机效应估计(Random Effects,简称RE)、固定效应估计(Fixed Effects,简称FE)、可行广义最小二乘估计(Feasible Generalized Least Squared,简称FGLS)和带面板校正标准误差的最小二乘估计(Panel Corrected Standard Errors,简称PCSE)、带DK(Driscoll-Kraay,简称DK)标准误的线性回归估计共6种估计模型。回归结果如表2所示。
表 2 相关方法的估计结果POLS RE FE FGLS PCSE DK lny −0.266 (−0.66) 0.229* (1.67) 0.272* (1.79) −0.302*** (−3.38) −0.266*** (−3.28) 0.272 (1.18) lny2 −0.366 (−0.57) 0.0850 (0.89) 0.110 (1.12) −0.587*** (−6.47) −0.366*** (−2.97) 0.110 (1.04) lnu 8.634 (0.79) −2.259* (−1.87) −2.357* (−1.93) 1.465 (0.99) 8.634** (2.07) −2.357*** (−3.47) lnu2 −1.081 (−0.78) 0.295* (1.82) 0.307* (1.87) −0.146 (−0.74) −1.081 (−1.96) 0.307*** (3.50) lne −0.178 (−1.28) 0.006 (0.26) 0.008 (0.31) −0.162*** (−6.55) −0.178*** (−4.98) 0.008 (0.49) lns21 0.112 (0.60) −0.125** (−1.97) −0.116* (−1.76) 0.101*** (2.72) 0.112** (2.18) −0.116** (−2.48) 常数项 −12.070 (−0.56) 8.602*** (3.74) 8.781*** (3.79) 1.489 (0.54) −12.070 (−1.55) 8.781*** (6.33) 样本数 420 420 420 420 420 420 个体效应 有 有 有 有 时间效应 有 有 有 有 有 有 调整后的判定系数 0.263 4 0.822 8 0.822 9 0.263 4 0.263 4 0.822 9 注:*、**、*** 分别代表变量回归系数在0.1、0.05和0.01水平上通过了显著性检验,括号内为标准差。 作为基准,本文首先基于POLS方法对全样本进行了估计,但结果并不显著(见表2)。由于面板数据包含截面异质性特征,因此POLS估计不可避免地会伴有异质性偏差。接下来,本文做了兼顾个体效应和时间效应的RE和FE估计(见表2)。并做了豪斯曼检验,结果表明统计量为27.06,在0.01水平上显著,FE方法更适用。但检验序列自相关的伍德里奇F检验表明,统计量为30.586,在0.01水平上显著,即存在自相关;而检验截面自相关的派尔森(Pesaran)CD检验也显示,统计量为−2.367,在0.05水平上显著,即存在截面自相关。而且,瓦尔德检验也显示,统计量为843.13,在0.01水平上显著,即FE模型存在组间异方差。为了纠正上述偏差,本文也使用了FGLS估计(见表2)。而本研究数据序列长度为14,远小于截面的个数30,这与FGLS估计样本时间长度至少与截面个数一样大的要求不相符,会造成估计结果存在不准确的可能,比如表2中城市化变量的一次lnu和二次项lnu2系数都不显著。因此,FGLS方法并不可靠。于是本研究又分别做了考虑存在“异方差-截面相关”的PCSE估计方法和考虑存在“异方差-截面相关-序列相关”稳健标准误时的DK估计(见表2)。不过,值得注意的是这些回归方法都假定解释变量对被解释变量的影响在不同截面上是恒定不变的,这有违样本存在异质性的可能。基于此,本研究在估计结果较好的固定效应模型基础上使用考虑异质性的门限回归模型。
三 门限回归结果
本文选择人均实际GDP作为分组的门限变量,确定门限变量阈值的个数及数值大小,并进行门限效应的检验。结果如表3。
表 3 门限检验假设分类 CV(95%) 类别 门限阈值 F值 置信区间(95%) Ho: 无门限 17.402 8 1个门限 1.066 1 147.762 7(0.000 0) [1.025 5, 1.086 4] Ha: 1个门限 Ho: 1个门限 17.638 8 2个门限 0.558 3 30.838 1(0.004 0) [0.517 6, 0.558 3] Ha: 2个门限 1.066 1 [1.025 5, 1.066 1]
Ho: 2个门限11.392 8 3个门限 0.558 3 44.536 7(0.000 0) [0.517 6, 0.558 3] 0.863 0 [0.863 0, 0.863 0] Ha: 3个门限 1.066 1 [1.025 5, 1.066 1] 注:CV值是基于自助法(bootstrap)抽样1 000次得到的,括号中为F统计量对应的P值。 人均实际GDP有3个阈值,分别是0.558 3,0.863 0和1.066 1,对应的人均实际GDP分别是17 477元、23 703元和29 040元。从而将30个省份分为低收入(y≤17 477)、中低收入(17 477<y≤23 703)、中高收入(23 703<y≤29 040)和高收入(y>29 040)4组(见表4)。
表 4 门限回归结果变量 低收入 中低收入 中高收入 高收入 lny −1.463 6
(0.975 0)2.093 9***
(0.719 2)−2.100 6**
(0.965 5)3.126 1***
(0.497 7)lny2 −0.891 0*
(0.510 0)1.708 3*
(0.928 3)−11.424 0
(7.384 8)−3.336 3***
(0.447 3)lnu 5.266 5***
(1.413 1)5.913 8***
(1.543 1)3.830 4**
(1.500 5)4.024 2***
(1.391 6)lnu2 −0.737 4***
(0.188 6)−0.778 4***
(0.216 8)−0.296 1
(0.211 3)−0.353 0*
(0.183 2)lne 0.170 8***
(0.037 9)0.028 2
(0.028 1)0.160 9***
(0.042 0)−0.006 7
(0.042 7)lns21 0.112 8
(0.108 7)0.343 7***
(0.089 3)0.227 7**
(0.093 9)0.370 0***
(0.090 5)样本数n 81 159 82 140 注:*、**、*** 分别代表变量回归系数在0.1、0.05和0.01水平上通过了显著性检验,括号内为标准差。 根据表4可以看出城市化水平与碳排放之间的关系,4组省份都呈现了库兹涅茨曲线的倒U型形状。从一次项系数来看,低收入与中低收入两组城市化的弹性系数分别是5.266 5和5.913 8,均大于中高收入与高收入两组的3.830 4和4.024 2。这说明人均实际GDP超过23 703元后,城市化引起的碳排放增加的幅度会减少。并且人均实际GDP介于17 477和23 703元之间的中低收入组,城市化引起碳排放增加的幅度最大。与人均实际GDP的一次项系数相比,4组城市化lnu的弹性系数均大于lny。相对于经济发展,这说明城市化是碳排放更大的驱动因素。
根据碳排放关于城市化的弹性系数公式
${E_u} = {\beta _2} + $ $ 2{\beta _3}\ln u$ ,我们得到低收入与中低收入组城市化EKC曲线的拐点值,城市化水平分别是35.55%和44.64%。库兹涅茨的倒U型形状说明,城市化首先带来碳排放的增加,增加到一定程度后开始减少。可能的解释是,城市化的人口集聚,首先带来巨大的交通与运输压力,而交通能耗是城市最大的碳源之一,特别是收入的提高带来的私人交通的井喷式发展;同时,城市化会大大拓展投入和产出活动在城乡之间长距离的运输链条,伴随着公路等交通方式、电力等公共网络的发展,产生大量的能耗和碳排放[24]。但城市也是解决气候变化的“钥匙”[25]。城市化带来的技术革新与资源优化,会大大改善能源的使用效率,提高清洁能源的比例,推动绿色可持续的生活方式迅速普及,从而将碳排放控制在一定范围。至于人均实际GDP与碳排放之间的关系,低收入组与中低收入组的非线性关系显著,但与库兹涅茨曲线假说的倒U型形状不一致;中高收入组的非线性关系并不显著;只有人均实际GDP大于29 040元的高收入组,其经济增长与碳排放之间呈现的是倒U形的库兹涅茨曲线形状。根据碳排放关于人均实际GDP的弹性系数公式
${E_y} = {\beta _0} + 2{\beta _1}\ln y$ ,我们得到高收入组经济发展EKC曲线的拐点值是人均实际GDP为15 976元。而由于高收入组的人均实际GDP已经超过29 040元,因此说,高收入组的经济发展EKC曲线已经处于倒U形曲线的下降阶段,即碳排放量水平会随着人均实际GDP的增加而减少。碳排放对国有能源工业固定资产投资的弹性系数,低收入组和中高收入组是显著的正值,分别为0.170 8和0.160 9(见表4),这说明节能减排投资尚没有发挥作用,仍然表现为固定资产投资带来的生产扩张的碳排放负效应。虽然高收入组的弹性系数为负的0.006 7,但由于数值较小且并不显著,因此,这说明现阶段几乎所有省份的节能减排投资尚未发挥对环境的正向作用。
对于用第二产业与第一产业的比值衡量的工业化对碳排放的影响,4组弹性系数分别为0.112 8、0.343 7、0.227 7和0.370 0(见表4)。这说明工业化水平每提升1%,碳排放会分别增加0.112 8%、0.343 7%、0.227 7%和0.370 0%。根据历史经验,一个国家的工业化进程必将伴随着劳动力从农业部门向城市工业部门的转移,同时商品从自给自足的小规模生产转化为商品交易的大规模生产,从而也伴随着化石能源的大量使用和碳排放增加[26-27]。其中,低收入组的弹性最小,即工业化的碳排放效应最小,可能的解释是低收入省份工业化初期占主导地位的产业仍是劳动密集型的轻工业,能耗排放的增加远小于产出的增加,即其产出效应远大于能耗产生的排放效应。
四. 结 论
本研究使用我国30个省份2003—2016年的面板数据,基于门限回归模型的建立分析我国城市化的温室效应。根据门限变量人均实际GDP,将30个省份分为小于17 477元的低收入组,介于17 477元和23 703元之间的中低收入组,介于23 703元和29 040元之间的中高收入组,以及大于29 040元的高收入组。研究结论表明,4组省份城市化与碳排放的关系都符合库兹涅茨曲线的倒U型形状。其中,人均实际GDP小于23 703元的低收入与中低收入两组的拐点,分别是城市化水平为35.55%和44.64%。4组中,只有人均实际GDP大于29 040元的高收入组,其经济增长与碳排放之间呈现的是倒U形的库兹涅茨曲线形状,而且处于倒U形曲线的下降阶段。碳排放对国有能源工业固定资产投资和第二产业与第一产业比值的弹性系数都是正值,这说明工业化进程与节能减排投资仍表现为对碳排放的扩张效应。
基于本文的研究结论,政策建议主要体现在以下两个方面:首先,在确定节能减排的省级分配目标时应该考虑到不同省份的经济发展水平、发展速度以及城市化程度对碳排放的不同影响。更进一步讲,应该考虑到不同省份劳动力、资本和能源资源等生产要素禀赋的差异,从而在节能减排投资与产业结构转移过程中更好地兼顾经济发展与环境规制的双重目标。其次,现阶段中国的节能减排战略与措施不能违背和脱离经济发展的阶段性特征和社会发展规律。城市化进程中,人口的空间移动和产业转移带来能源和碳排放的大量增加,迫切需要政府进行宏观管理的顶层设计,将城市低碳化与工业绿色化进程嵌入到经济发展的战略目标中;实现经济发展的同时,促进供给侧能源更为清洁和再生,促进产业结构低碳升级;在需求侧倡导更加环保节能的城市生活理念和消费方式,实现经济增长、节能减排与社会和谐的协调发展。
-
表 1 面板单位根检验
变量 LLC同单位根检验 IPS异单位根检验 水平序列 一阶差分序列 水平序列 一阶差分序列 lnC −7.838
(0.010)−16.537
(0.000)−1.397
(0.718)−2.733
(0.000)lnu −6.167
(0.000)−17.225
(0.000)−1.597
(0.305)−2.702
(0.000)lnu2 −6.551
(0.000)−16.675
(0.000)−1.543
(0.415)−2.630
(0.000)lny −4.005
(0.594)−14.297
(0.002)−1.025
(0.995)−2.410
(0.000)lny2 −5.297
(0.045)−18.029
(0.000)−1.120
(0.981)−3.102
(0.000)lne −9.332
(0.000)−17.998
(0.000)−1.656
(0.203)−2.940
(0.000)lns21 −7.279
(0.002)−12.758
(0.000)−1.499
(0.509)−2.284
(0.000)注:表中的数值为Z统计量值,括号内为相应的P值。 表 2 相关方法的估计结果
POLS RE FE FGLS PCSE DK lny −0.266 (−0.66) 0.229* (1.67) 0.272* (1.79) −0.302*** (−3.38) −0.266*** (−3.28) 0.272 (1.18) lny2 −0.366 (−0.57) 0.0850 (0.89) 0.110 (1.12) −0.587*** (−6.47) −0.366*** (−2.97) 0.110 (1.04) lnu 8.634 (0.79) −2.259* (−1.87) −2.357* (−1.93) 1.465 (0.99) 8.634** (2.07) −2.357*** (−3.47) lnu2 −1.081 (−0.78) 0.295* (1.82) 0.307* (1.87) −0.146 (−0.74) −1.081 (−1.96) 0.307*** (3.50) lne −0.178 (−1.28) 0.006 (0.26) 0.008 (0.31) −0.162*** (−6.55) −0.178*** (−4.98) 0.008 (0.49) lns21 0.112 (0.60) −0.125** (−1.97) −0.116* (−1.76) 0.101*** (2.72) 0.112** (2.18) −0.116** (−2.48) 常数项 −12.070 (−0.56) 8.602*** (3.74) 8.781*** (3.79) 1.489 (0.54) −12.070 (−1.55) 8.781*** (6.33) 样本数 420 420 420 420 420 420 个体效应 有 有 有 有 时间效应 有 有 有 有 有 有 调整后的判定系数 0.263 4 0.822 8 0.822 9 0.263 4 0.263 4 0.822 9 注:*、**、*** 分别代表变量回归系数在0.1、0.05和0.01水平上通过了显著性检验,括号内为标准差。 表 3 门限检验
假设分类 CV(95%) 类别 门限阈值 F值 置信区间(95%) Ho: 无门限 17.402 8 1个门限 1.066 1 147.762 7(0.000 0) [1.025 5, 1.086 4] Ha: 1个门限 Ho: 1个门限 17.638 8 2个门限 0.558 3 30.838 1(0.004 0) [0.517 6, 0.558 3] Ha: 2个门限 1.066 1 [1.025 5, 1.066 1]
Ho: 2个门限11.392 8 3个门限 0.558 3 44.536 7(0.000 0) [0.517 6, 0.558 3] 0.863 0 [0.863 0, 0.863 0] Ha: 3个门限 1.066 1 [1.025 5, 1.066 1] 注:CV值是基于自助法(bootstrap)抽样1 000次得到的,括号中为F统计量对应的P值。 表 4 门限回归结果
变量 低收入 中低收入 中高收入 高收入 lny −1.463 6
(0.975 0)2.093 9***
(0.719 2)−2.100 6**
(0.965 5)3.126 1***
(0.497 7)lny2 −0.891 0*
(0.510 0)1.708 3*
(0.928 3)−11.424 0
(7.384 8)−3.336 3***
(0.447 3)lnu 5.266 5***
(1.413 1)5.913 8***
(1.543 1)3.830 4**
(1.500 5)4.024 2***
(1.391 6)lnu2 −0.737 4***
(0.188 6)−0.778 4***
(0.216 8)−0.296 1
(0.211 3)−0.353 0*
(0.183 2)lne 0.170 8***
(0.037 9)0.028 2
(0.028 1)0.160 9***
(0.042 0)−0.006 7
(0.042 7)lns21 0.112 8
(0.108 7)0.343 7***
(0.089 3)0.227 7**
(0.093 9)0.370 0***
(0.090 5)样本数n 81 159 82 140 注:*、**、*** 分别代表变量回归系数在0.1、0.05和0.01水平上通过了显著性检验,括号内为标准差。 -
[1] 赵可,张雄,张炳信. 城市化与城市建设用地关系实证−基于中国大陆地区1982—2011年时序数据[J]. 华中农业大学学报(社会科学版),2014(2):107-113. [2] 林伯强, 姚昕, 刘希颖. 节能和碳排放约束下的中国能源结构战略调整[J]. 2010(1): 58-71. [3] 吴婵丹,陈昆仑. 国外关于城市化与碳排放关系研究进展[J]. 城市问题,2014(6):22-27. [4] 邱立新,徐海涛. 基准情境与干扰情境下中国典型城市碳排放趋势预测[J]. 城市问题,2019(3):12-22,83. [5] JORGENSON A K,CLARK B. Assessing the temporal stability of the population /environment relationship in comparative perspective:a cross-national panel study of carbon dioxide emissions,1960-2005[J]. Population and Environment,2010,32(1):27-41. doi: 10.1007/s11111-010-0117-x
[6] DRUCKMAN A,CHITNIS M,SORRELL S,et al. Missing carbon reductions? exploring rebound and backfire effects in UK households knowledge[J]. Energy Policy,2011(39):3572-3581.
[7] POUMANYVONG P,KANEKO S. Does urbanization lead to less energy use and lower CO2 emissions? a cross-country analysis[J]. Ecological Economics,2010,70(2):434-444. doi: 10.1016/j.ecolecon.2010.09.029
[8] MARTINEZ-ZARZOSO I,MARUOTTI A. The impact of urbanization on CO2 emissions:evidence from developing countries[J]. Ecological Economics,2011,70(7):1344-1353. doi: 10.1016/j.ecolecon.2011.02.009
[9] 胡碧霞,李菁,匡兵. 绿色发展理念下城市土地利用效率差异的演进特征及影响因素[J]. 经济地理,2018,38(12):183-189. [10] 周少甫,蔡梦宁. 城市化、碳排放与经济增长关系的实证分析[J]. 统计与决策,2017(2):130-132. [11] 方齐云,曹金梅. 城市化、产业结构与人均碳排放[J]. 天津财经大学学报,2016(5):77-88. [12] 赵钊,于寄语. 城市化与二氧化碳排放[J]. 城市问题,2015(12):19-25. [13] LI K,LIN B Q. Impacts of urbanization and industrialization on energy consumption/CO2 emissions:does the level of development matter?[J]. Renewable and Sustainable Energy Reviews,2015,52:1107-1122. doi: 10.1016/j.rser.2015.07.185
[14] LI H N,MU H L,ZHANG M,et al. Analysis of regional difference on impact factors of China’s energy-related CO2 emissions[J]. Energy,2012,39(1):319-326. doi: 10.1016/j.energy.2012.01.008
[15] WANG Y,ZHAO T. Impacts of energy-related CO2 emissions:evidence from under developed,developing and highly developed regions in China[J]. Ecological Indicators,2015,50:186-195. doi: 10.1016/j.ecolind.2014.11.010
[16] ZHANG C G,LIN Y. Panel estimation for urbanization,energy consumption and CO2 emissions:a regional analysis in China[J]. Energy Policy,2012,49:488-498. doi: 10.1016/j.enpol.2012.06.048
[17] EHRHARDT-MARTINEZ K. Social determinants of deforestation in developing countries:a cross-national study[J]. Social Forces,1998,77(2):567-586. doi: 10.2307/3005539
[18] 余东华,张明志. “异质性难题”化解与碳排放EKC再检验−基于门限回归的国别分组研究[J]. 中国工业经济,2016(7):57-73. [19] CHENERY H, ROBINSON S, SYRQUIN M. Industrialization and growth: a comparative study[M]. New York:Oxford University Press, 1986.
[20] YORK R,ROSA E A,DIETZ T. STIRPAT,IPAT and ImPACT analytic tools for unpacking the driving forces of environmental impacts[J]. Ecological Economics,2003,46(3):351-365. doi: 10.1016/S0921-8009(03)00188-5
[21] GROSSMAN G M, KRUEGER A B. Environmental impacts of a North American Free Trade Agreement[EB/OL]. [2019-12-15]. http://www.nber.org/papers/w3914.
[22] DINDA S. Environmental Kuznets Curve hypothesis:a survey[J]. Ecological Economics,2004,49(4):431-455.
[23] HANSEN B E. Threshold effects in non-dynamic panels:estimation,testing,and inference[J]. Journal of Econometrics,1999,93(2):345-368. doi: 10.1016/S0304-4076(99)00025-1
[24] 秦昌才. 经济增长门限效应下的城市化与碳排放[J]. 烟台大学学报(哲学社会科学版),2019(1):105-114. [25] 何建坤,卢兰兰,王海林. 经济增长与二氧化碳减排的双赢路径分析[J]. 中国人口·资源与环境,2018,28(10):9-17. [26] 陈占明,吴施美,马文博. 中国地级以上城市二氧化碳排放的影响因素分析:基于扩展的STIRPAT模型[J]. 中国人口·资源与环境,2018,28(10):45-54. [27] 范建双,周琳. 城镇化及房地产投资对中国碳排放的影响机制及效应研究[J]. 地理科学,2019,39(4):644-653. -
期刊类型引用(5)
1. 王鑫,陆大伟. 锂离子电池正极材料生产过程物流系统研究. 中国储运. 2024(10): 198-199 .  百度学术
百度学术
2. 薛俭,刘露露. 基于省际贸易视角的隐含碳权定价研究. 生态经济. 2022(11): 27-35 .  百度学术
百度学术
3. 熊萍萍,曹书人,杨卓. 华东地区碳排放量灰色关联度分析. 大连理工大学学报(社会科学版). 2021(01): 36-44 .  百度学术
百度学术
4. 王小元. 江浙沪城市立体绿化在应对温室效应中的作用. 华中建筑. 2021(03): 131-134 .  百度学术
百度学术
5. 刘胜粤. 广西能源消费碳排放动态特征及影响因素分析. 中国市场. 2021(16): 7-12 .  百度学术
百度学术
其他类型引用(11)
计量
- 文章访问数: 1938
- HTML全文浏览量: 802
- PDF下载量: 114
- 被引次数: 16



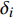
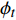
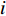
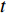
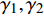
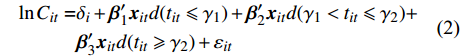
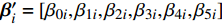
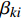
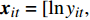
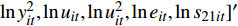
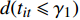
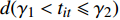
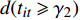
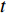
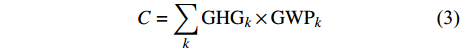
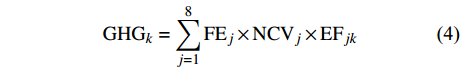
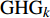
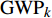
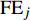

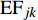
 下载:
下载: